행렬(Matrix)
- 일반적으로 2차원인 경우 행렬이라고 함
- 3차원 이상은 텐서
행렬의 정의
- m * n (row * column) 직사각형 모양으로 배열한 것
- 여기서 m * n이 행렬의 크기임
여기서 i열 j행의 원소를 a(아래첨자)ij 라고 하며 성분이라고도 함
행렬의 종류
1. 정방행렬 (Square Matrix)
행과 열의 수가 같은 것
주대각성분: 행열이 같은 숫자를 가지는 a()mn들의 집합?
2. 영행렬(Zero Matrix)
모든 성분이 0인 행렬
3. 단위행렬(Identity Matrix)
주대각성분이 1이고 나머지는 0인 것
I 또는 E로 표기함
4. 삼각행렬(Triangular Matrix)
정방행렬 중 주 대각선 아래 또는 위가 모두 0인 것
상삼각행렬: 정방행렬 중 주 대각선 아래가 모두 0인 것
하삼각행렬: 정방행렬 중 주 대각선 위가 모두 0인 것
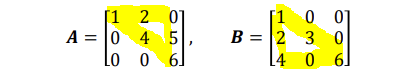
5. 대각행렬(Diagonal Matrix)
주대각성분을 제외한 모든 성분이 0인 행렬
상삼각행렬이자 하삼각행렬로 분류가능
6. 전치행렬(Transpose Matrix)
행렬의 모든 행을 대응하는 열과 바꾼 행렬
행렬 A의 전치 행렬은 A^T로 표기
걍 돌린다고 생각하면 편할듯?
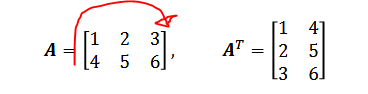
2행 3열인 애가 3행 2열로
7. 대칭행렬(Symmetric Matrix)
A = A^T인 행렬
정방행렬의 일종
8. 반대칭행렬(Antisymmetic Matrix)
A = -A^T인 행렬
9. 역행렬(Inverse Matrix)
AB = BA = I(단위 행렬) 일 때 A와 B는 서로의 역행렬
10. 직교행렬(Orthogonal Matrix)
A^T(전치행렬)*A = I(단위행렬)또는 A^-1 = A^T 가 성립하는 정방행렬
(어떤 행렬의 행 벡터와 열 벡터가 유클리드 공간의 정규 직교를 이루는 행렬)
직교행렬을 구성하는 열벡터는 크기가 1이며 서로 직교
직교행렬을 구성하는 행벡터의 크기가 1이며 서로 직교
* 직교성(Orthogonal): 독립의 충분조건. 직교하면 독립함(역은 성립하지 않음)
* 선형 독립(linear independence): 집합의 각 원소가 다른 원소로 설명할 수 없을 때 선형 독립이라고 함(진짜 독립적일 때)


만약 2차원 공간에서 본다면 a벡터를 k배 해서 b벡터를 만들 수 없음. 이런 것이 선형 독립이라고 함
여기서 직교는 독립의 한 케이스가 됨 왜냐하면
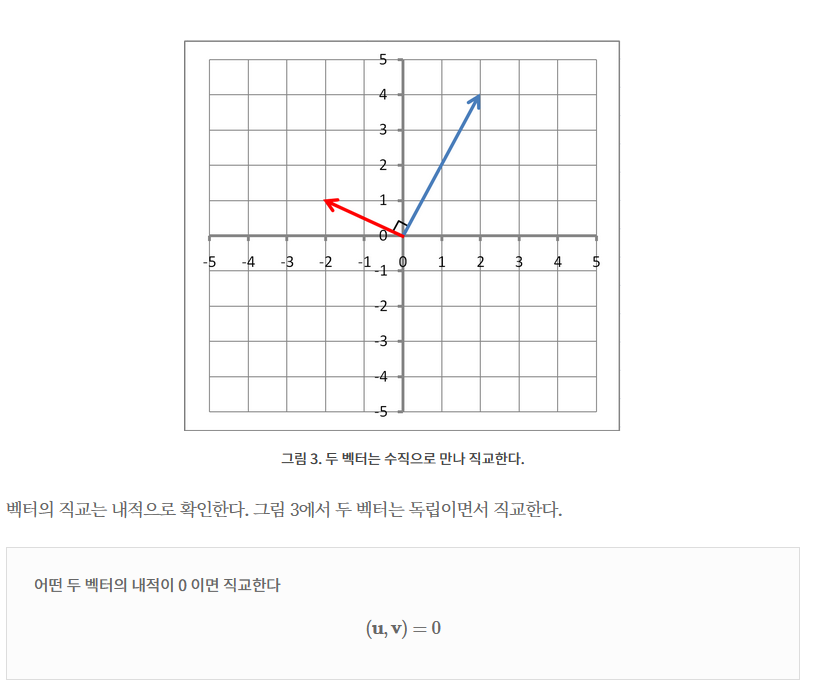
이런식으로 직교하면 독립이 되기 때문에
근데 사실 n차원 공간에서 서로 독립일 수 있는 벡터가 n개 뿐이라는게 좀 이해가 안가는 부분이다 왜냐하면
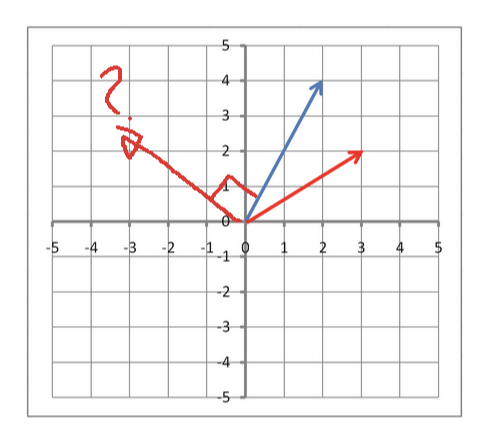
이렇게 하면 파란색 벡터는 2개의 독립벡터를 가지게 되는 것 아닌가? 근데 사실 그렇게 치면 파란색 벡터의 독립 벡터는 무한개가 되기는 한다. 이건 내가 이해를 잘못했거나 뭔가 예시가 잘못됐거나 둘 중 하나일듯.
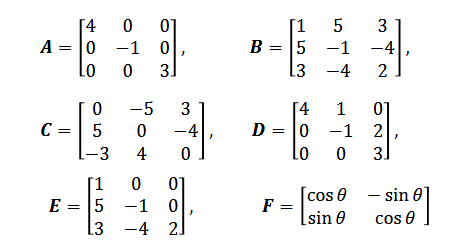
다음 각 행렬에서 정방행렬, 일행렬, 영행렬, 단위행렬, 대칭행렬, 반대칭행렬, 상삼각행렬, 하삼각행렬, 대각행렬, 직교행렬인지 파악해보자
A = 정방행렬, 대칭행렬, 상삼각행렬, 하삼각행렬, 대각행렬
B = 정방행렬, 대칭행렬
C = 정방행렬, 반대칭행렬
D = 정방행렬, 상삼각행렬 (아래가 0인게 상삼각이다 아래가 없다고 생각하자)
E = 정방행렬, 하삼각행렬 (반대)
F = 정방행렬, 직교행렬(행렬의 곱셈은 1행 * 1열, 1행 * 2열, 2행 * 1열, 2행 * 2열 이렇게 진행함 사실 전부 다 곱하는 것임)
참고로 F는 회전행렬이라고 하며 회전은 길이를 변형하지 않으면서 방향만 바꾸는 변환임. 즉 길이를 그대로 보존하기 때문에 직교행렬이 된다고 하는데.. 한 50%는 무슨 소리인지 모르겠다
행렬의 덧셈 A+B
두 행렬의 크기가 같을 경우에만 정의
위치가 같은 각 원소끼리만 더함
[a(ij) +- b(ij)](i=1 ~ m, j = 1 ~ n)
행렬의 스칼라배 kA
각 원소를 k배 A행렬이 m * n 일 경우
k[a(ij)](i= 1 ~ m, j = 1 ~ n)
행렬의 곱셈 A*B
A의 크기가 m * p, B의 크기가 p * n 일 때만 정의 (A의 열의 개수와 B의 행의 개수가 같아야 함 이는 내적계산을 하기 위해서임)
(이는 선형대수학의 선형변환과 행렬 사이의 함수의 합성과 행렬 곱을 자유롭게 오갈 수 있도록 하기 위해서)
AB의 크기는 m * n
결국 A의 행을 곱한다는 것은 1행의 열 값을 곱한다는 거고, B의 열을 곱한다는 것은 1열의 행 값을 곱한다는 것임
이때 열 값과 행 값이 같아야지 곱셈이 된다는 것
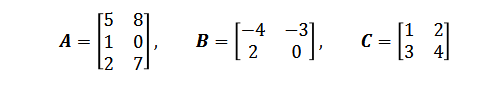
-2A = [-10, 16/ -2, 0/ -4, -14]
B+C = [-3, -1/ 5, 4]
AB = [-4, -15/ -4, -3/6, -6]
* 내적과 외적
내적 (a⋅b=∣a∣∣b∣cosθ)
벡터에는 방향이 있으며 일치하는 만큼 곱한다 (적(쌓을적)은 곱한다는 것)
이때 서로 방향이 90도가 되면 내적의 값은 0이 된다 (직교?하면 I가 되는 것과 같은 개념?)
결과값은 스칼라로 나옴
컴퓨터 그래픽이나 기계학습을 할 때 벡터의 방향이 얼마나 비슷한지 측정할 때 사용, 정사영(projection) 계산
벡터의 내적은 얼마나 같은 방향인가(사이각 알아보기?)를 알아보기 위해 (같은 방향을 향하는 정도라는 스칼라 찾기)
외적 (a×b=∣a∣∣b∣sinθn)
벡터를 곱하는 또 다른 방법으로 방향은 A, B 벡터의 수직이고 크기는 두벡터가 이루는 정사각형의 넓이임
결과값은 벡터로 나옴
3D 그래픽, 물리학에서 회전 방향 계산/각속도(애니메이션, 로봇공학)할 때 사용
벡터의 내적은 얼마나 수직한가(방향)를 알아보기 위해 (수직한 방향이라는 새로운 벡터 찾기)
요약
1. 행렬의 곱은 A행렬의 열 값과 B행렬의 행 값이 같아야 곱셈이 가능 하며 이때 AB의 크기는 A의 행(m) * B의 열(n)
2. 단위 행렬은 주성분이 1이고 나머지 성분이 0인 행렬, I또는 E라고 표시 (Identity matrix)
3. 전치행렬은 행렬의 모든 행을 대응하는 열로 바꾸는 것 열은 행으로 바꾸고. A^T 라고 함
이때 대칭행렬은 A = A^T, 반대칭행렬은 A = -A^T
4. 직교행렬은 A^T * A = I (스칼라가 0)/ A^T = A^-1일 때를 말하며 직교할 때는 선형독립함(A원소로 B원소를 설명할 수 없음) 단 역은 성립하지 않음
5. 내적은 사이각, 스칼라를 구하기 위해 사용하는 벡터의 곱셈이고 외적은 수직벡터를 알아보기 위해 사용하는 벡터의 곱셈이다
'코딩의 기록' 카테고리의 다른 글
| 따라하며 배우는 파이썬과 데이터과학 10장 심화문제 (0) | 2025.02.18 |
|---|---|
| 따라하며 배우는 파이썬과 데이터과학 -10.넘파이로 수치 데이터를 처리해보자 (0) | 2025.02.17 |
| 따라하며 배우는 파이썬과 데이터과학 9장 심화문제 (0) | 2025.02.15 |
| 따라하며 배우는 파이썬과 데이터과학 -9. 텍스트를 처리해보자- (0) | 2025.02.13 |
| 따라하며 배우는 파이썬과 데이터과학 8장 심화문제 (1) | 2025.02.02 |