1. 리스트보다 넘파이의 배열이 훨씬 빠르다
넘파이 배열은 리스트보다 처리속도가 압도적으로 빠르다
넘파이: 대용량의 배열과 행렬연산을 빠르게 수행하며, 고차원적인 수학 연산자와 함수를 포함하고 있는 파이썬 라이브러리임 판다스나 기계학습을 위한 Scikit-learn, Tensorflow가 넘파이 위에서 작동하기 때문
넘파이의 핵심적인 객체는 다차원 배열. 배열의 각 요소는 인덱스라고 불리는 정수들로 참조됨. 차원은 축(axis)라고 부름.
2. 리스트와 넘파이의 배열은 무엇이 다른가
넘파이는 ndarry(n-dimension-array) 객체를 제공 ndarry는 n차원 배열을 의미
배열은 동일한 자료형을 가진 데이터만 저장, 리스트는 동일하지 않은 자료형을 가진 항목들을 담을 수 있음
1. ndarry는 c언어 기반 배열 구조라서 메모리를 적게 차지하고 속도가 빠름
2. ndarray는 배열과 배열 간의 수학적인 연산을 적용 가능
3. ndarray는 고급 연산자와 풍부한 함수들을 제공
넘파이는 더하기를 하면 대응하는 원소들끼리 더해짐
3. 넘파이의 별칭 만들기, 그리고 간단한 배열 연산하기
import numpy as np로 별칭을 만들고
np.array(list) array()함수에 리스트를 전달하면 넘파이 배열이 생성됨
넘파이 +는 두 넘파이 배열의 대응되는 원소끼리 더하여 같은 크기의 배열에 담음
import numpy as np
a = np.array(range(1, 11))
b = np.array(range(10, 101, 10))
print(a+b)
print(a-b)
print(a*b)
print(a/b)
4. 넘파이의 핵심 다차원배열을 알아보자
넘파이 배열이 ndarry이고 ndarry는 다차원배열임
a.shape # a객체의 형태 열과 행의 개수 (3,) 1은 따로 표기하지 않음 튜플형
행렬을 구분하는 방법은 그냥 위에 걸로 예시를 들면 "4. 넘파이의 핵심 다차원 배열을 알아보자"가 1행임 그리고 1열은
"4넘a" 그러니까 1열 2행이라고 하면 넘이고 1행 2열이라고 하면 .임
a.dim a객체의 축, 차원
a.dtype 내부 자료형 파이썬 표준 자료형도 사용할 수 있고 넘파이 자체 자료형도 사용 가능
a.itemsize 내부 자료형이 차지하는 메모리크기 byte int는 4byte 8bit = 1byte
a.size 전체 크기, 항목의 수 shape의 m, n의 곱과 같음
a.data 배열의 실제 원소를 포함하고 있는 버퍼
a.stride(보폭) 배열 각 차원별로 다음 요소로 점프하는 데에 필요한 거리를 바이트로 표시한 값을 모은 튜플
참고로 전부다 상수임 메소드 아님(리턴하는 거 아님)
import numpy as np
a = np.array(range(1, 11)) + np.array(range(10, 101, 10))
print(a.shape)
print(a.size)import numpy as np
array_a = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array_b = np.array(range(0, 10))
array_c = np.array(range(0, 10, 2))
print("실습 1 :", array_a)
print("실습 2 :", array_b)
print("실습 3 :", array_c)
print("array_c의 shape :", array_c.shape)
print("array_c의 ndim :", array_c.ndim)
print("array_c의 dtype :", array_c.dtype)
print("array_c의 size :", array_c.size)
print("array_c의 itemsize :", array_c.itemsize)
5. 강력한 넘파이 배열의 연산을 알아보자
스칼라값을 넘파이 배열에 +, * 할 수 있음
넘파이 계산이 빠른 이유: 자료형이 다 같아서 > 데이터 항목에 필요한 저장공간이 일정하기에 순서만 알면 바로 접근 가능해서(임의 접근, random access) 주기억 장치로 많이 쓰는 기억장치가 RAM(random access memory) 기억장치가 회전하면서 원하는 위치의 데이터를 읽는 하드디스크보다 빠름
import numpy as np
height = [1.83, 1.76, 1.69, 1.86, 1.77, 1.73]
weight = [86, 74, 59, 95, 80, 68]
npheight = np.array(height)
npweight = np.array(weight)
BMI = npweight / (npheight * npheight)
print("대상자들의 키:", npheight)
print("대상자들의 몸무게:", npweight)
print("대상자들의 BMI:", BMI)넘파이 배열은 ** 연산도 가능하다 그리고 넘파이 배열은 신기하게 print로 그냥 출력하면 콤마가 없음 그냥 리스트는 콤마를 출력하는데
6. 인덱싱과 슬라이싱을 넘파이에서도 할 수 있다
리스트와 같음
7. 논리적인 인덱싱을 통해 값을 추려내자
논리적인 인덱싱(logical indexing): 어떤 조건을 주어서 배열에서 원하는 값을 추려내는 것
ages = np.array([18, 19, 25, 30, 18])
y = ages > 20 (논리연산자 사용가능!) >> [False, False, True, True, True] 이렇게 부울형의 넘파이 배열을 리턴함
ages[ages > 20] 이렇게 하면 부울형 배열을 인덱스로 ages[]로 보내게 되고 그러면 array[]
리스트에는 안되는 기능이고 넘파이에서만 되는 기능인데 넘파이 배열은 부울형 배열을 인자로 받을 수 있음
부울형 배열을 받으면 True 위치의 값만 가져옴
이게 되는 이유는 넘파이의 고급인덱싱 방법이다
참고로 브로드캐스팅(Broadcasting)은 크기가 다른 배열끼리 연산할 때, Numpy가 자동으로 크기를 맞춰서 연산하는 기능임 가상의 확장으로 연산하기 때문에 메모리 낭비가 없음
8. 2차원 배열 인덱싱도 해 보자
파이썬의 리스트의 리스트가 2차원 행렬임
넘파이 배열에서 행렬 연산이 가능함
np_array[행, 열](넘파이 스타일 슬라이싱), np_array[행],[열](파이썬 리스트 슬라이싱)
9. 넘파이는 넘파이 스타일로 인덱싱할 수 있다
row행을 가져온 뒤 col번째 항목을 찾는 것이 아니라 바로 접근하는 것임을 명심
10. 넘파이 스타일의 2차원 배열 잘라내기
np_array[0:2, 2:4]
0에서 1까지의 행에서 2에서 3까지의 열을 잘라내라는 의미
np_array[::2][::2] vs np_array[::2, ::2] (파이썬 리스트 슬라이싱 vs 넘파이 스타일 슬라이싱)
그냥 간단하게
전자는 배열 2개를 가져 온 다음 (여기서 배열 2개를 가진 배열이 되고) 그러면 0번째 배열, 1번째 배열 중 0번째 배열만 가져오는 것이고
후자는 그냥 바로 접근하는 거 처럼 행 자르고 열 잘라서 가져오는 것
11. 2차원 배열에서 논리적인 인덱싱을 해보자
2차원 배열에서 논리 연산을 사용하게 되면 1차원 행렬이 추출됨(미분?)
부울형 배열을 얻어낸 다음 이거를 다시 2차원 배열에 넣으면 얻고 싶은 결과를 낼 수 있는듯
import numpy as np
x = np.array([['a', 'b', 'c', 'd'], ['c', 'c', 'g', 'h']])
y = x[:] == "c"
y = x[y]
mat_a = np.array([[10, 20, 30], [10, 20, 30]])
mat_b = np.array([[2, 2, 2], [1, 2, 3]])
print(y)
print(mat_a + mat_b)
차원(dimension)은 어떤 수치 데이터를 다룰 때 고려해야 하는 속성이 몇 개인지에 따라 결정됨
예) 3차원 공간은 x, y, z축을 알아야지 정확한 지점을 알 수 있음 즉 정확히 말하면 n개를 고려해야지 원하는 답이 나올 경우 그것을 n차원이라고 하는듯
1차원 배열을 벡터(vector)라고 함 벡터는 원소의 개수가 차원이 됨
[1, 4], [3, 2, 1] 모두 1차원 배열이지만 벡터로 간주하면 1차원 데이터가 2와 3개씩 있는 2차원 벡터, 3차원 벡터임
벡터의 차원은 몇 개의 항목이 있는지에 따라 결정되고 배열의 차원은 몇 가지 방향으로 줄이 있는지를 표현하는 것
2차원 배열은 축이 2개 있는 것으로 이러한 데이터를 행렬(matrix)이라고 부르며 각각의 축을 행(row)과 열(column)이라고 함
3차원 배열이 표현하는 데이터는 텐서(tensor)라고 함
그러나 텐서는 모든 차원의 배열을 포괄하는 개념으로 벡터는 1차원 텐서, 행렬은 2차원 텐서라고 할 수 있음
그러니까 다시 말하자면
1차원 배열 > 벡터 (텐서)
2차원 배열 > 행렬 (텐서)
3차원 배열 이상 > 텐서(텐서는 포괄적인 개념)
벡터의 차원과 배열의 차원은 다르다 차원 자체는 축(새로운 방향)을 새로 만들어야 늘어남
벡터의 차원은 수학적 차원으로 수학에서 차원은 원소의 개수임
1차원 배열을 벡터라고 부르는 이유는 1차원 배열이 벡터의 성질과 유사한 면이 있기 때문 (배열연산과 벡터연산)
즉 행렬은 벡터를 원소로 가질 수 있음
import numpy as np
x = np.array([[1.83, 1.76, 1.69, 1.86, 1.77, 1.73], [86.0, 74.0, 59.0, 95.0, 80.0, 68.0]])
y = x[0:2, 1:3]
z = x[0:2][1:3]
print("x shape :", x.shape) #형태라는 뜻이 shape을 말하는 거였음 더 정확하게 말하면 전체적인 모양? (m, n)
print("y shape :", y.shape)
print("z shape :", z.shape)
print("z values = :", z)
print("BMI data")
print(x[0])
print(x[1])
print(x[1] / x[0]**2)import numpy as np
players = [[170, 76.4], [183, 86.2], [181, 78.5], [176, 80.1]]
np_players = np.array(players)
print("몸무게가 80 이상인 선수 정보")
print(np_players[np_players[:, 1] >= 80.0 ]) # 행만 자를 땐 [n] 표현이 가능하지만 열을 자를 땐 [, n]은 안되고 [:, n] 이런식으로 해야함
print("키가 180 이상인 선수 정보")
print(np_players[np_players[:, 0] >= 180])
넘파이가 진짜 개쩌는게 내가 원하는 곳에만 조건을 검사할 수 있고 그 원하는 것이 true일 때 그 행/열을 출력하는 것도 해준다
12. arrange() 함수와 range() 함수의 비교
특정한 범위의 정수를 가지는 넘파이 배열을 만들 수 있음
numpy.arrange(start, stop, step)
range()를 통해 생성된 것은 반복 가능 객체 iterable임
13. linspace() 함수와 logspace() 함수
numpy.linspace(start(생략 불가), stop(stop까지 생성됨), num = 50)
시작값부터 끝값까지 균일한 간격으로 지정된 개수만큼을 배열의 값으로 생성함
arrange()는 정수만 가능하고 linspace는 실수도 가능한 차이가 ㅣㅆ는 듯
numpy.logspace(start, stop, num = 50)
로그 스케일로 수들을 생성함 간격이 로그 스케일 기본은 10^x ~ 10^y 까지이며 base 인자에 따라 2^x, 3^x로 바꿀 수 있음
14. 배열의 형태를 바꾸는 reshape() 함수와 flatten() 함수
new_array = old_array.reshape(shape)
reshape()는 데이터의 개수는 유지한채로 배열의 차원과 형태를 변경함
shape를 튜플 형태로 넘겨주는 것이 원칙이지만 x,y로 넘겨줘도 (x,y)와 동일하게 처리함
데이터의 개수는 유지하므로 m*n = l*k가 되어야만 바꿀 수 있음
인수로 -1을 전달하면 데이터의 개수에 맞춰서 자동으로 배열의 형태가 결정됨
y = np.arrange(12)
y.reshape(6, -1) >> 열은 2가 됨
flatten()은 평탄화 함수로 2차원 이상의 고차원 함수를 1차원 배열로 만들어줌
15. 난수를 생성해보자
어떤 확률 분포에서 난수를 생성하여서 실험 데잍로 사용할 수도 있음
random number
난수(random number): 무작위성(randomness)의 특징을 가지고 출현하는 수를 의미함
여기서 무작위성이란 특정한 패턴이 존재하지 않아 다음에 어떤 수가 나타날지 예측할 수 없다는 것
자연에서 진짜 난수를 얻어내는 방법은 쉽지 않음 대기나 열에서 발생하는 잡음, 양자 현상, 우주 배경 복사 등
일반적으로 컴퓨터 프로그래밍에서는 의사 난수(pseudo random number)를 사용함 이 난수함수는 동일한 시드가 주어지면 동일한 난수를 생성하게 됨
16. 난수 생성하기
규칙성이 전혀 없는 난수의 열은 컴퓨터로 생성하는 것이 불가능함 규칙으로 규칙이 없는 랜덤을 만들어내는 것은 불가능하기 때문
사실 컴퓨터는 아주 기능이 많은 계산기일 뿐이다
그래서 의사난수(pseudo random number)를 만듦
시드는 컴퓨터로 만드는 난수의 초기 입력값으로 사용됨
np.seed(100)
>> 이걸로 난수의 초기 입력값을 주고
np.random.rand(행, 렬)
>> 난수는 0.0 ~ 1.0 사이의 값으로 생성됨
np.random.randint(1, 11, size = (행, 렬))
>> 정수 난수 생성
17. 정규 분포 난수 생성
앞의 rand, randint는 균일한 확률 분포로 생성됨
특정 구간에서 난수를 생성하면 해당 구간 전체에서 골고루 데이터가 나타나게 됨
하지만 많은 사건들의 발생의 확률은 정규분포를 띔
정규분포는 평균(파이)과 표준편차(시그마)가 주어짐
낮아지는 정도는 표준편차와 관계가 있음 표준편차가 크면 클수록 데이터의 흩어짐이 크기 때문에 발생 확률이 평평하게 퍼진 상태에 접근하게 됨
randn(행, 렬)
난수들의 평균은 0이고 표준편차가 1이 되는 표준정규분포가 되도록 난수들이 나옴
평균은 그래프의 위치를 결정하고 표준편차(분산, 표준편차의 제곱)는 폭을 결정함
즉 평균값 mu를 가지고 표준편차 sigma를 가지는 정규분포를 생성하고 싶다면
mu + sigma * np.random.randn()을 하면 됨 즉 이 정규분포는 mu와 sigma 값에 따라 모양이 바뀌는데
이때 요래저래 계산해보면 표준편차를 바꾸고 싶다면 sigma를 곱하면 되고 평균값을 바꾸고 싶다면 mu를 더하면 됨
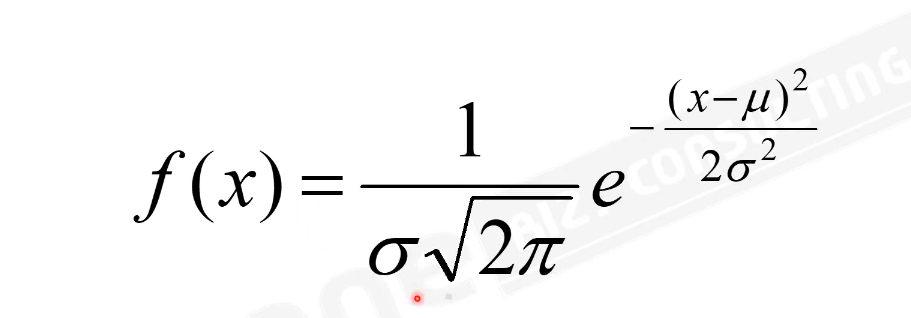
18. 평균과 중앙값 계산하기
중앙값(median): 리스트의 중앙에 있는 항목 이상치(outlier) 때문에 전체의 평균 값이 전체의 대표성을 가지지 못하는 경우를 막기 위해 사용됨
mean() 평균계산
median() 중앙값 구함
import numpy as np
players = np.zeros((100, 3))
players[:, 0] = np.random.randn() * 10 + 175
players[:, 1] = np.random.randn() * 10 + 70
players[:, 0] = np.floor(np.random.randn()) * 10 + 175
print("신장 평균값:", players[:, 0].mean) #축을 통해도 가능한데 np.mean(player, axis = n)[m]으로 모든 열의 평균을 구한뒤 m열을 가져올 수 있음 제시한 방법보단 메모리 소모가 있을 수 있음
print("신장 중앙값:", players[:, 0].median)
print("체중 평균값:", players[:, 1].mean)
print("체중 중앙값:", players[:, 1].median)
print("나이 평균값:", players[:, 2].mean)
print("나이 중앙값:", players[:, 2].median)n차원 배열은 축이 n개가 있는 것 가장 작은 n번째 축이 가장 바깥의 축이 됨
np.zeros()는 배열을 0으로 채워서 만들 때 사용
19. 상관관계 계산하기
키-몸무게, 재력-차 같은 의존성의 정도가 상관관계임
corrcoeff(x, y)함수는 요소들의 상관관계를 계산함 이때 x, y는 데이터를 담고 있는 리스트나 배열이 될 수 있음
수학적으로 피어슨(Pearson) 상관 계수를 계산하는 함수임
x-x 상관관계 Cxx
x-y 상관관계 Cxy
y-x 상관관계 Cyx
y-y 상관관계 Cyy
음의 상관관계일 경우 -1, 상관관계가 전혀 없을 때 0, 양의 상관관계가 있을 때 1
이 행렬에서 Cxx와 Cyy는 자기 자신과의 매칭이므로 항상 1의 값을 가짐
그리고 Cxy와 Cyx는 같은 것이므로 대칭행렬을 가짐
20. 다수 변수들 사이의 상관관계 계산하기
다수의 변수들의 상관관계를 확인하려면 리스트들을 리스트로 묶어서 호출해야함
result = np.corrcoef( [x, y, z] )
입력된 데이터를 행렬로 인식해야 하기 때문 x, y는 그냥 행렬로 자동으로 인식해주는 모양인듯?
요약
1. 넘파이는 ndarray 배열을 제공하며 리스트보다 성능이 좋고 메모리도 적게들고 여러곳에서 쓰임
2. 행은 그냥 생각하는 거처럼 가로가 행이 맞고 세로가 열이다 근데 헷갈리는 이유는 분명 가로가 행이라고 했는데 셀때는 세로로 세기 때문에 근데 그것도 잘 생각해보면 별로 의문가질 일은 아니다
3. shape(배열의 모양 행 열이 몇개인지 등), ndim(축이 몇 개인지), size(전체 요소)
4. 넘파이는 임의 접근 (Random Access)이기 때문에(자료형이 다 같아서 순서만 알면 바로 접근가능) 빠르고 넘파이식과 리스트식 슬라이싱이 다름 [ , ] vs [][]
5. 논리 인덱싱이 가능하고 고급 인덱싱이 가능하여 부울형 배열을 인자로 받을 수 있음 또한 열 행 만 따로 검사하여 만족하는 배열을 출력하는 기능도 가능
6. 브로드캐스팅으로 크기가 다른 배열은 자동으로 크기를 맞춰서 연산도 해줌
7. 1차원 배열: 벡터, 2차원 배열: 행렬(매트릭스) 1, 2차원 포함 3차원 이상: 텐서 그리고 벡터는 수학적인 의미로 원소의 개수에 따라 1차원 벡터 2차원 벡터로 표현함 이렇게 벡터 매트릭스 텐서로 부르는 이유는 배열 연산이 이런 연산들과 거의 비슷하기 때문
8. range()는 iterable객체를 만듦 넘파이에서는 arrange() / 실수는 linspace(), 로그는 logspace() range와 다른 점은 시작점을 생략 불가하고 stop까지 생성한다는 점이 다름
9. reshape()는 데이터 개수를 변경하지 않고 배열의 모양을 바꿔줌, flatten()은 1차원 배열로 만들어줌
10. 컴퓨터는 난수와 비슷한 기능을 하는 의사난수(pseudo random number)를 만드는데 먼저 초기값이 되는 시드seed()를 주면 rand() 0 ~ 1 까지, randint()로 정수 난수 생성가능
11. 위의 것들은 균일하게 난수가 주어지지만 되게는 정규분포 형태를 띄기 때문에 randn이 필요 mu = 0, sigma = 1인 표준정규분포 데이터를 생성함 만약 둘을 조정하고 싶다면 sigma는 곱하고, mu는 더해서 조정가능
12. 평균값은 mean(), 중앙값은 median()을 사용하여 구할 수 있음 참고로 중앙값은 이상치(outlier)를 잡아내기 위해 사용
13. n차원 배열에서 가장 작은 축(0)은 가장 바깥쪽 축임 zeros()로 요소가 0인 배열을 만들 수 있음
14. corrcoeff(행, 렬) 함수로 리스트 간의 상관관계를 볼 수 있음 행렬로 받기 때문에 3개 이상은 리스트로 묶어서 행렬로 만들어줘야 함 참고로 대각선은 전부 1이고 역의 관계들은 대칭행렬이 됨
'코딩의 기록' 카테고리의 다른 글
| 행렬 (1) (0) | 2025.03.12 |
|---|---|
| 따라하며 배우는 파이썬과 데이터과학 10장 심화문제 (0) | 2025.02.18 |
| 따라하며 배우는 파이썬과 데이터과학 9장 심화문제 (0) | 2025.02.15 |
| 따라하며 배우는 파이썬과 데이터과학 -9. 텍스트를 처리해보자- (0) | 2025.02.13 |
| 따라하며 배우는 파이썬과 데이터과학 8장 심화문제 (1) | 2025.02.02 |